General research interests

My main interests lie in the field of sequential decision making under uncertainty. This field studies methods that allow an intelligent system, an agent, to make decisions over time. I am particularly interested in multiagent systems. Sequential decision making is studied in, and has close ties to many research fields within AI, CS and economics such as: planning, reinforcement learning, optimization, machine learning, regression, classification, graphical models, probabilistic inference and game theory.

Particular topics of study

Some topics that I have done research on:

• Decentralized POMDPs: theory, optimal and approximate planning methods.
• Exploiting structure in graphical models of interactions.
• Reinforcement learning for teams of agents.
• Smartly coordinating traffic lights.
• Reasoning about trust in e-commerce settings via POMDPs.
• Mining social structures: dealing with entity resolution, and exploratory support for historical databases.
• Team decision making with delayed communication.
• Poker formalized as POMDPs.

Research Highlighted

A selection of some research contributions, including slides.

Simulation-based Planning using Deep Q-learning for Traffic Light Control

Better traffic light control in urban settings could have great impact on quality of living. In some recent research I have been investigating the applicability of deep reinforcement learning techniques to improve traffic flow.

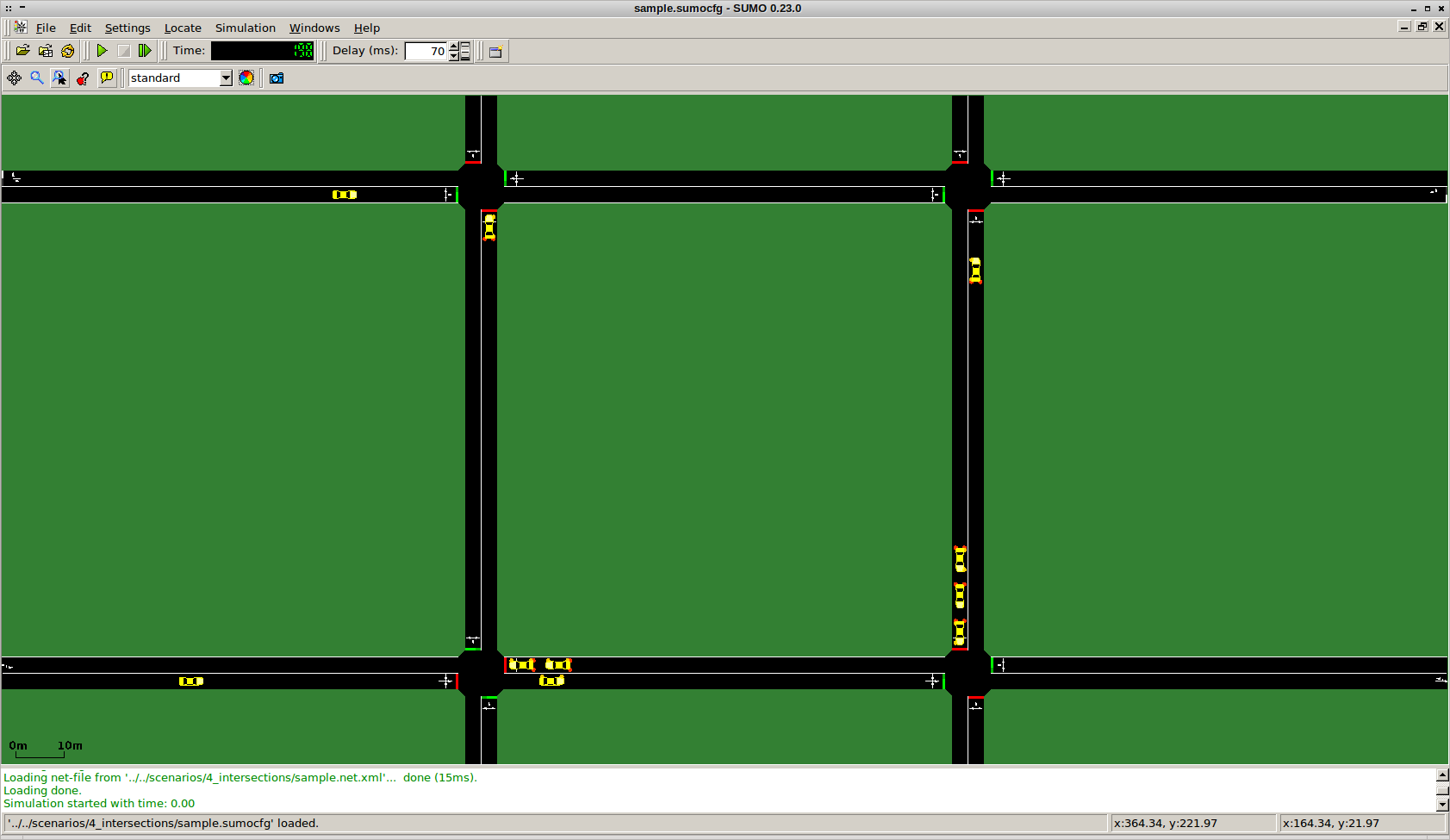
In particular, in her MSc project Elise van der Pol has shown that the DQN algorithm can be applied for the control of one and two intersection problems. The latter can than be used in a coordinated approach, by building on a variant of transfer planning (further described below). The results are quite exciting, as a video (link below) shows this new approach might allow for higher traffic densities without complete congestion, when compared to a state-of-the-art other coordination approach (the approach by Kuyer et al. 2008).

For more information, see...

• the video demonstrating our transfer planning + deep Q-learning approach
• the BNAIC video demo paper

Advances in Optimal Solutions for Dec-POMDPs

The optimal solution of Dec-POMDPs is a notoriously hard problem. Yet, the field is making steady progress in solving larger POMDPs.

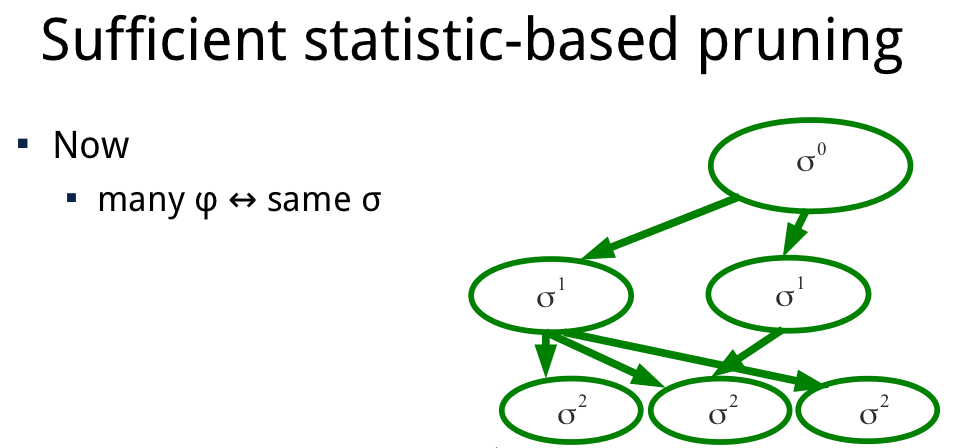
Incremental clustering and incremental expansion are two techniques that are introduced in our JAIR'13 article that have greatly expanded the range of problems that can be solved optimally. More recently, I found a reformulation of optimal value functions based on sufficient statistics that may enable more compact representations of those value functions and potentially can lead to speed ups.

For more information, see...

• the presentation I gave at CWI and UIC.
• the JAIR paper
• the IJCAI paper

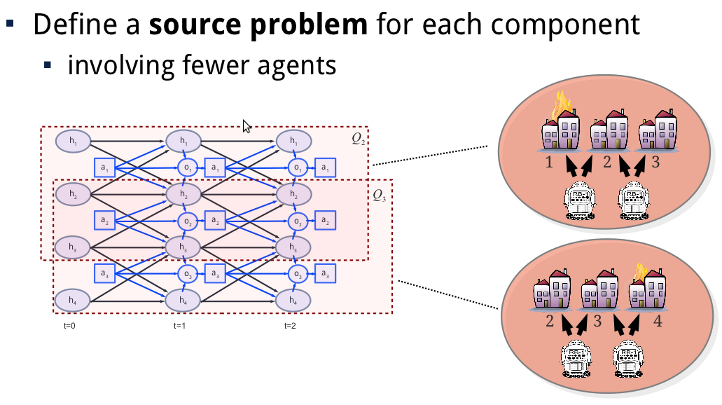
Approximate Solution of Factored Dec-POMDPs via Transfer Planning

In recent work we have introduced transfer planning, a method to compute a factored heuristic for factored Dec-POMDPs. By using this in a factored version of forward-sweep policy computation, we can scale to hundreds of agents.

The main idea behind transfer planning is that we approximate the original problem using a set of multiple abstractions, each involving subsets of agents. The value functions of these so-called source problems, can then be transfered to the original problem.

For more information, see...

• the paper
• the citation
• the AAMAS presentation.