Together with Thomas Kipf, Max Welling and myself, Elise van der Pol did some excellent work on model-based RL.
See:
- This post on plannable approximations with MDP homomorphisms
- The paper
Month: March 2020
Plannable Approximations to MDP Homomorphisms: Equivariance under Actions
If you need meaningful latent representations for MDPs for e.g. planning or exploration, have a look at our AAMAS 2020 paper. We use a contrastive loss to learn MDP homomorphisms.
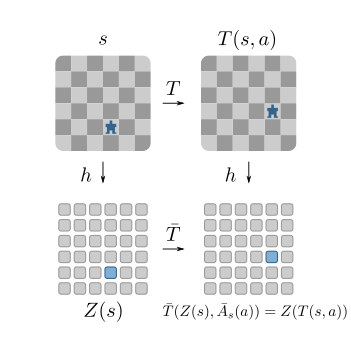
An MDP homomorphism is a structure-preserving map from an input MDP to an abstract MDP (the “homomorphic image”). MDP homomorphisms maintain the optimal Q-values and thus the optimal policy.
Roughly speaking, we find a smaller abstract representation of our MDP, and if the map is an MDP homomorphism, the optimal policy is guaranteed to be the same.
We prove that as the loss function reaches 0, we find an MDP homomorphism for deterministic MDPs. This is attractive because we could in theory plan in a reduced MDP and lift to the optimal policy in the original, bigger MDP!
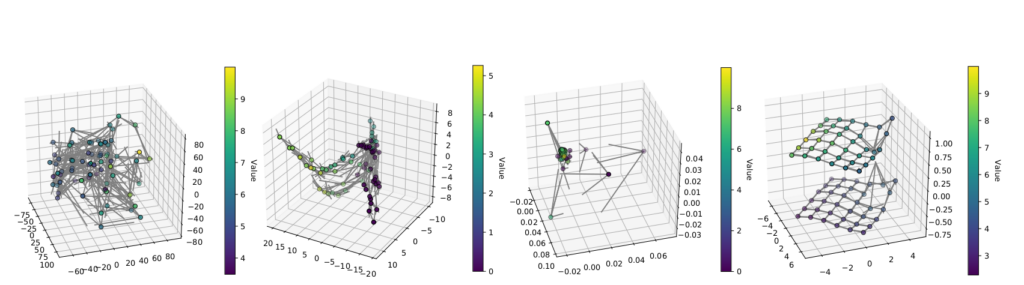
Due to the homomorphism constraints, we learn much better structured representations (rightmost figure), which support better planning. We show empirically that the policy found in the abstract MDP performs well in the original MDP.